The Coefficient of Variation (CV) is a way of measuring the variability of a series of numbers. It is calculated by dividing the standard deviation by the mean of the observed values.
Why use it?
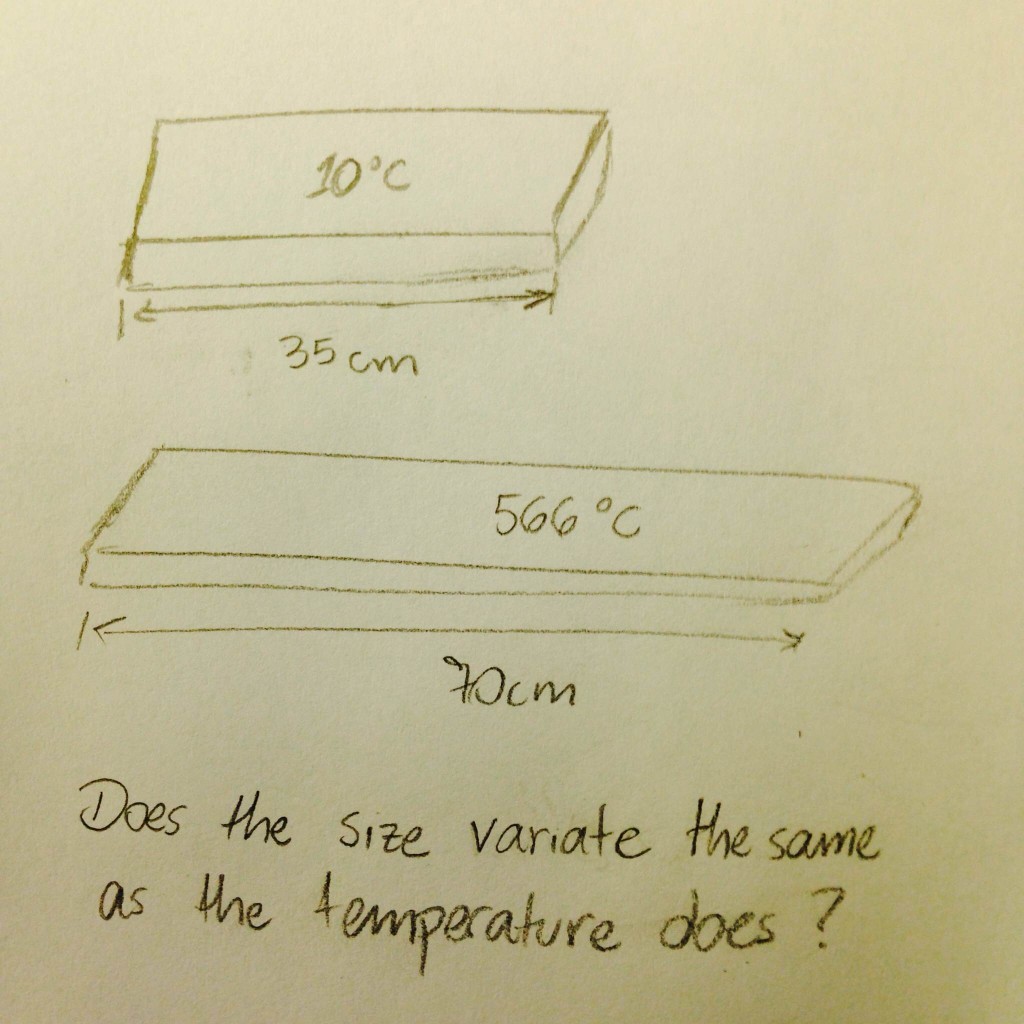
It is used for comparing different kinds of measurements in an experiment. For example, it makes possible seeing if the variation in the temperature was the same as the variation in the size of an object.
A very simple use would be to check if an object becomes twice bigger when it is twice hotter.
However, the CV can do more than this. It enables the comparison between the variations after many observations.
In case of comparing values of the same unit of measurement, the standard deviation is enough.
Restriction
The CV should not be calculated using interval scale, only range scale.
Using temperature values as a reference, the following lines show why this is a restriction.
What is temperature?
It is the average of the thermal energy from all particles in a system. In other words, it is a measurement of energy. It means that having three times more energy (without varying the number of particles) results on a temperature three times higher.
What is a degree?
According to the dictionary, it is any of a series of steps or stages. For example, a degree Celsius is a hundredth of the temperature change between the freezing and the boiling points of the water.
Comparing Celsius vs. Fahrenheit
If we assume that 20ºC represents twice more energy than 10ºC, it is easy to check that Fahrenheit fails to calculate it. Those values in Fahrenheit would be, respectively, 68ºF and 50ºF and it is easy to see that at least one of them is wrong. On the other hand, we might assume that 40ºF represents twice more energy than 20ºF and the values in Celsius would be, respectively, -6.6ºC and +4ºC.
It is important to notice that making those assumptions are wrong because Celsius and Fahrenheit are interval and not range scales. Something at 20ºC has, actually, 3,5% more energy than another thing at 10ºC, for example.
What is Kelvin?
It is an absolute unit of measurement. The value 0K means total absence of energy, it is called as a ratio scale. Because this, an object at 200K has twice more energy than an object at 100K.
Using this idea, it is possible to check that 20ºC (293K) does not mean a temperature twice bigger than 10ºC (283K), but the real relation would be represented by 293/283 (= 1,035).
Kelvin vs. ºX
Let’s define any temperature aºX as b + 1000ºC, so it will never be negative.
If we compare 200K (= -73ºC = 927ºX) with 100K (= -173ºC = 827ºX), it is easy to see that 927ºX / 827ºX does not show the real variation, since 927ºX has actually twice more energy than 827ºX.
Kelvin vs. Rankine
Rankine (ºRa) is a unit of measurement which has the zero value at the same point as Kelvin does: at total absence of heat. On the other hand, each degree Rankine has the same size as a degree Fahrenheit.
This means that 200K = 111,11ºRa and 100K = 55,55ºRa. The calculation is done by multiplying to 5/9.
The relation 111,11/55,55 shows that the first is two times bigger than the latter and particularly allows its use to calculate the CV.
Short example
Having two measurements x and y, where x = 2y, we can calculate:
Mean = 1,5y
Standard deviation = [(2y – 1,5y)2 + (y – 1,5y)2]1/2
CV = 0,3333
Finally, if an object had temperature 100K and now it is 200K and its size changed from 35cm to 70cm, both CVs will be 0,3333 and it is possible to say that the different units of measurement have had the same variation, because the CVs have the same value.
References
Coefficient of Variation: Charles E. Brown. Coefficient of variation. In Applied Multivariate Statistics in Geohydrology and Related Sciences, pages 155–157. Springer Berlin Heidelberg, 1998.


